Contenido
En esta publicación, consideraremos qué es una combinación lineal de cadenas, cadenas linealmente dependientes e independientes. También daremos ejemplos para una mejor comprensión del material teórico.
Definición de una combinación lineal de cadenas
Combinación lineal (LK) término s1Con2, …, sn matriz A llamada expresión de la siguiente forma:
αs1 + as2 + … + αsn
Si todos los coeficientes αi son iguales a cero, entonces LC es trivial. En otras palabras, la combinación lineal trivial es igual a la fila cero.
Por ejemplo: 0·s1 + 0·s2 + 0·s3
En consecuencia, si al menos uno de los coeficientes αi no es igual a cero, entonces LC es no trivial.
Por ejemplo: 0·s1 + 2·s2 + 0·s3
Filas linealmente dependientes e independientes
El sistema de cuerdas es linealmente dependiente (LZ) si existe una combinación lineal no trivial de ellos, que es igual a la línea cero.
Por lo tanto, se deduce que una LC no trivial puede, en algunos casos, ser igual a la cadena cero.
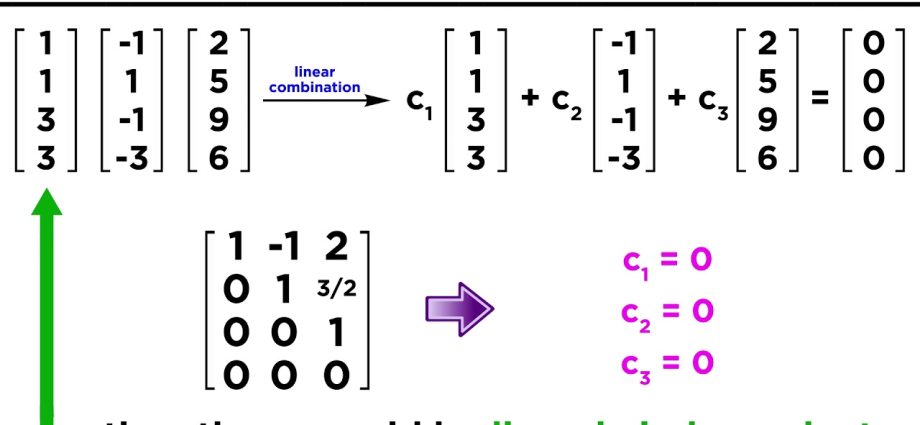
El sistema de cuerdas es independiente linealmente (LNZ) si solo la LC trivial es igual a la cadena nula.
Notas:
- En una matriz cuadrada, el sistema de filas es un LZ solo si el determinante de esta matriz es cero (las = 0).
- En una matriz cuadrada, el sistema de filas es un LIS solo si el determinante de esta matriz no es igual a cero (las ≠ 0).
Ejemplo de un problema
Averigüemos si el sistema de cuerdas es
Decisión:
1. Primero, hagamos una LC.
α1{3 4} + un2{9 12}.
2. Ahora veamos qué valores deben tomar α1 и α2para que la combinación lineal sea igual a la cadena nula.
α1{3 4} + un2{9 12} = {0 0}.
3. Hagamos un sistema de ecuaciones:
![]()
4. Divide la primera ecuación por tres, la segunda por cuatro:
![]()
5. La solución de este sistema es cualquier α1 и α2, Con α1 = -3a2.
Por ejemplo, si α2 = 2luego α1 = -6. Sustituimos estos valores en el sistema de ecuaciones anterior y obtenemos:
![]()
Respuesta asi que las lineas s1 и s2 linealmente dependiente.